Synapse and Dendrites

Google Search of SETI Net

Synapses

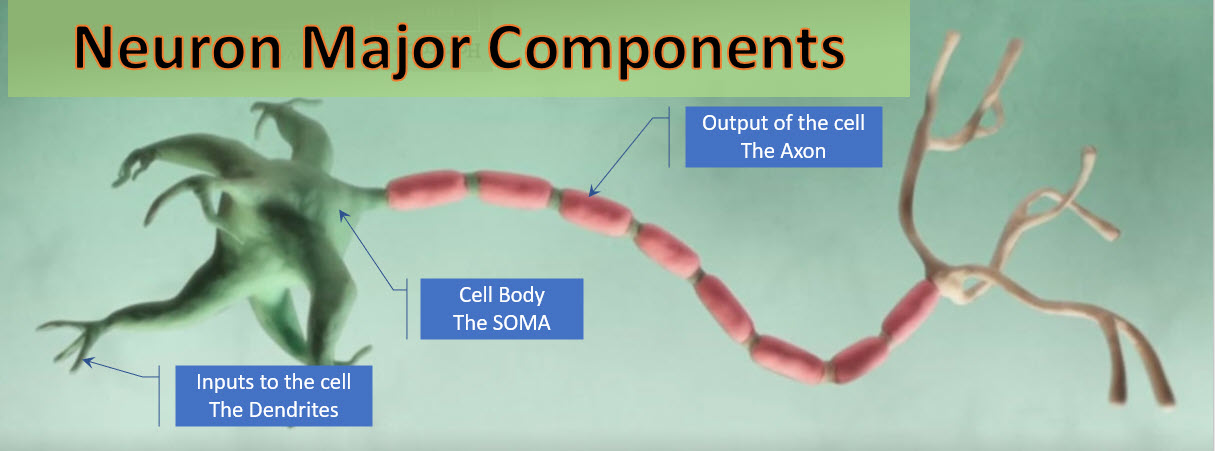
The connection between two neurons is called a synapse. Since each neuron can connect to thousands of other neurons, each neuron has many thousand synapses.

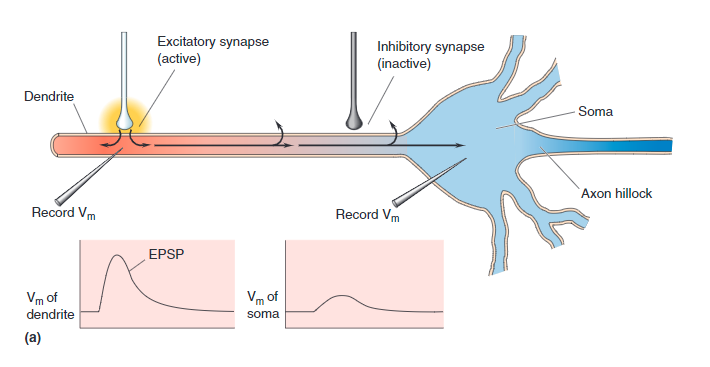
The drawing below shows a single neuron with a driving Axon on the left and a receiving Synapse on the right. The PREsynaptic terminal is on the left, and the POSTSynaptic terminal on the right.

Synaptic terminals are physically at the end of each axon. The terminal is the place where the pulse of chemicals, the action potential, is converted into a neurotransmitter release. The Synapse membrane is less than 50 nanometers away and contains specialized receptors. The neurotransmitter rapidly (in microseconds) diffuses across the synaptic cleft and binds to specific receptors. The type of neurotransmitter released from the terminal and the specific receptors present on the synapse are critical in determining the quality and intensity of information transmitted by neurons. The synaptic and Dendrites of the neuron integrates all the signals it receives to determine what it does next, for example, to fire an action potential of its own or not.

The Neuron Lab simulator does not simulate to the level of the synapse neurotransmitters. In this simulator, the synapses' role is in support of the phenomenon of Spike Timing Delay Plasticity (STDP), which is described in the section on STDP. In this simulator, the synapse is considered to have a dendrite cylinder connected to it. If you check the parameters of a synapse (right-click on one), you can see the Length and Diameter settings. These are for the dendrite portion of the synapse. You can also see a check box marked ISPS. If set, the synapse acts as an Inhibitory Postsynaptic Potential (IPSP) input to the dendrite cell.[kandel page 275 *]

The box marked STDP contains a slider that, when this function is installed in the simulator, will show the amount of boost or buck applied to this synapse. For this release the slider is non-functional.

Dendrites

The Dendrites are the inputs to the neuron cell. They have extensive arborization and, in the case of the Purkinje cells, connect to hundreds of thousands of other cells. Normally, they are connected to about 10,000 cells[kandel Page 337 *]. The neuron cell membrane contains ion channels that allow specific ions to flow through the lipid bilayer and we treated the neuron cells as small round objects. But neuron cells are not small round objects. They contain these major areas

Postsynaptic terminal
Dendrites
The Soma (cell body)
The Axon
Presynaptic terminal

This is one of the most famous images in neurobiology.

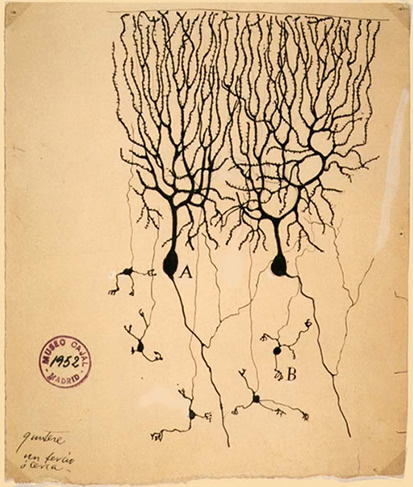
Two Purkinje neurons hand drawn by Santiago Ramon y Cajal at the turn of the 20th century

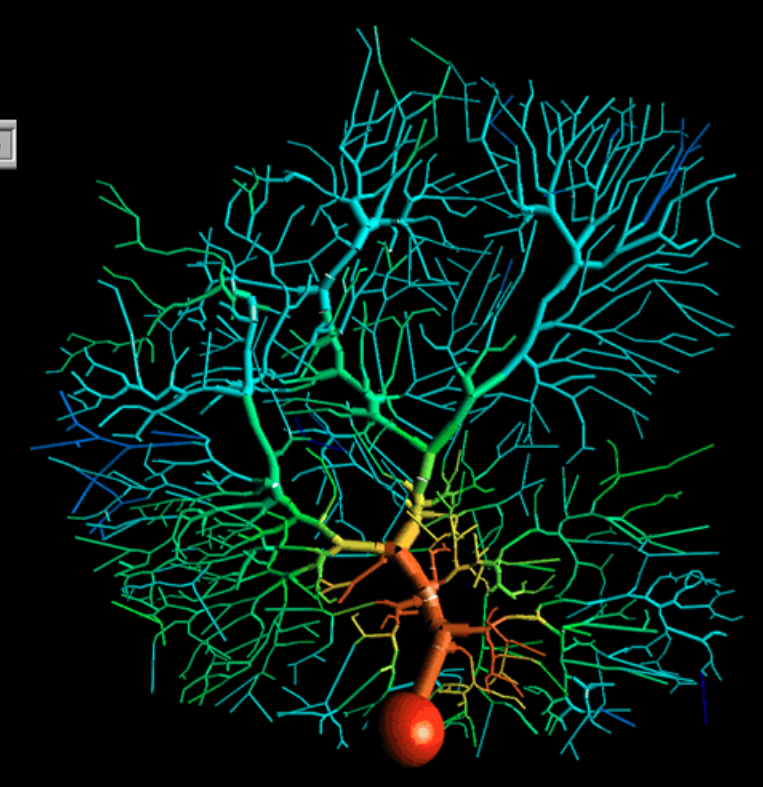
The neuron Soma is the physically largest part of the neuron. It typically has a diameter of 100 uM. The diameter of the dendrites may be down to 1 uM or less. The dendrites usually extend 100's of microns, but some can extend several meters, as in the giraffe brain.

Branching - Dendrites tend to bifurcate repeatedly and create (often several) large and complicated trees. Cerebellar Purkinje cells typically bear one very complicated tree with approximately 400 tips. Cells from cat spinal cord usually have 8-12 trees each with approximately 30 terminal tips.

Diameters - Dendrites are thin tubes of nerve membrane. Near the soma they start with a diameter of few um and fall below 1 um as they successively branch.[Genesis chapter 5]

Length - Dendritic trees may range from very short (100-200 um) to quite long (1-2 mm) and the total dendritic length may reach 1 cm and more.[Genesis chapter 5]

Area and Volume - The majority of the brain volume and area is occupied by dendrites. The surface area of a single dendritic tree is in the range of 2,000 to 750,000 C_um. Volume may reach up to 30,000 um ³ .

This is a capture of a detailed multi-compartmental model of a cerebellar Purkinje cell , created with GENESIS simulator. It shows an input spike coming into the dendritic tree and spreading out as it moves down to the soma (the orange ball). The output of the soma is through a single axon ( not shown).

Compartments

A neuron and its dendrite tree is simplified for analysis with twelve compartments plus a soma and axon:

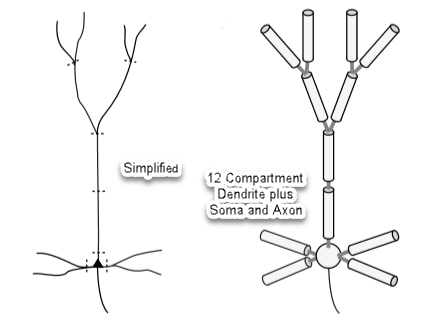
Dendrite compartments can be thought of Leaky Electrical Cables with capacitance. A single compartment is modeled below.

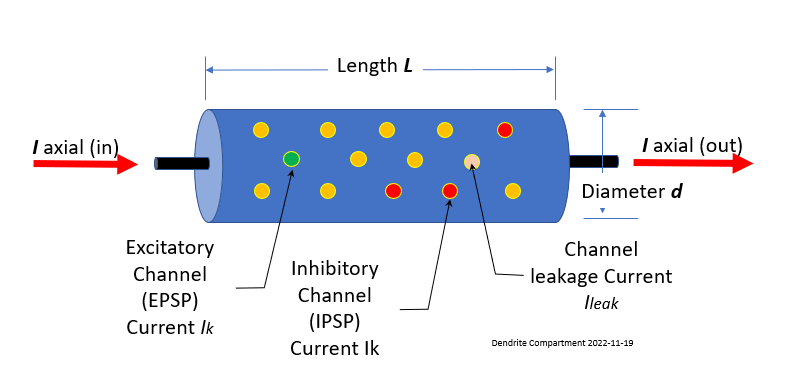
The ion channels are as described in 1.0 Cells and Ions. The inner conductor, the cytoplasm, is a much poorer conductor than the copper wire used in an undersea cable. It has a resistance along the length of the cable Ra, the "axial resistance." The conducting cytoplasm inside the cylinder, the insulating neural membrane, and the liquid (similar to salt water) surrounding the neuron form a capacitance Cm.

The membrane is also not a perfect insulator due to the ion-conducting channels that pass through it, allowing it to leak. The "passive channels" do not vary in conductance, and the "active channels" have conductances varying with voltage, calcium concentration, or synaptic input. The passive channels account for the membrane resistance Rm and the associated leakage current Ileak.

At first glance, the concept of 'leaking' may seem like a flaw in the system, but upon closer inspection, you'll discover that what you perceive as 'bugs' are actually adaptive features that enable our brains to function in a remarkably complex manner.

Compartment Electrical Equivalent

The various components of the cell compartment can be thought of as an electrical circuit and can be analyzed as such.

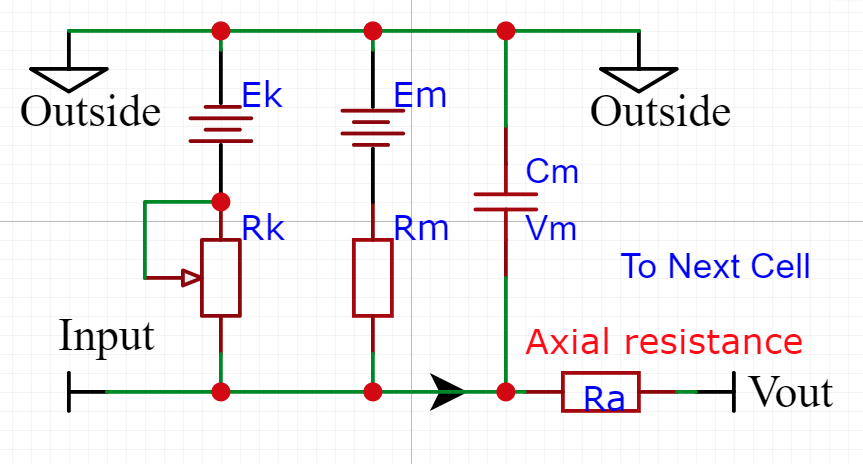
This drawing allows us to think of the cell in a way that we can reconcile that the inside of the cell is negative with respect to the Outside. Imagine hooking the ground side of your DVM to the Outside of the cell and then probing around at the inside points. You would see negative voltage levels only.

The simplest cable equation is the steady state where you can ignore the current flowing into the membrane capacitance C_m. The membrane voltage is given by $V_{m} = I_{m} R_{m}$ (membrane current times the membrane resistance).

Dimensions and units of measure

Specific units - To specify parameters that are independent of the compartment dimensions, specific units are used in this simulator.

For a cylindrical compartment, the membrane resistance is inversely proportional to the area of the cylinder, so we define a specific membrane resistance RM and the specific axial resistance RA, to have units of ohms cm². The membrane capacitance is proportional to the area, so it is expressed in terms of a specific membrane capacitance CM, with units of ufarads/cm².

Note the use of caps for RM, CM, and RA. This designates them as specific units.

If you wish to experiment with other values of specific units they are accessible through the menu of the simulator.

Range of Specific Membrane Resistance (RM ):

The specific membrane resistance (RM ) of neurons, typically measured in ohms square centimeters (Ω⋅cm² ), varies depending on the type of neuron, ion channel density, and other factors such as the cell's physiological state and location.

Typical: 5,000 ohm ⋅ cm² -This wide range reflects the diversity of neuron types and their varying surface area and ion channel distributions.
Small Neurons (e.g. Interneurons): 30,000 ohm⋅cm² to 100,000 ohm⋅cm²
Large Neurons (e.g. Pyramidal and Motor Neurons) : 5,000 ohm⋅cm² to 30,000 ohm⋅cm²

Examples:

Cortical Pytramidal Neurons : around 20,000 to 60,000 ohm⋅cm²
Purkinje Cells (Cerebellum) : low end. Around 5,000 to 20,000 ohm⋅cm²
Hippocampal Neurons (CA1): within 20,000 to 80,000 ohm⋅cm²

Factors Influencing RM:

Ion Channel Density: A higher density of ion channels (such as potassium and leak channels) generally decreases RM.
Membrane Surface Area: Larger surface areas with similar channel densities will have lower specific membrane resistance.
Physiological Conditions: RM can be modulated by synaptic activity, neuromodulation, temperature, and other cellular conditions

Range of Specific Axial Resistance (RA ):

The specific axial resistance (RA), also known as the internal or cytoplasmic resistance of the neuron, is usually expressed in ohms per centimeter (Ω⋅cm) because it relates to the resistance of the cytoplasm along the length of axons or dendrites. Here's the typical range and details of specific axial resistance:

Typical: 50 ohm⋅cm to 300 ohm⋅cm- This range is fairly standard across various neuron types and is influenced by factors such as the neuron's diameter, cytoplasmic composition, and ion mobility.
Smaller Dendrites: 200 to 300 ohm⋅cm - Smaller diameters result in higher resistance to the flow of current along the neurite due to a smaller cross-sectional area.
Larger (Axons): 50 to 150 ohm⋅cm - Larger axons, such as those found in motor neurons or myelinated fibers, have lower resistance due to a larger cross-sectional area that facilitates easier current flow.

Factors Influencing RA:

Diameter : The axial resistance is inversely proportional to the cross-sectional area; hence, larger diameters result in lower RA.
Cytoplasmic Properties: The ionic composition, viscosity, and overall quality of the cytoplasm can alter the resistance.
Temperature: Higher temperatures can reduce RA by increasing the mobility of ions within the cytoplasm.

Range of Specific Membrane Capacitance (CM):

The specific membrane capacitance (CM) of neurons is a measure of the membrane's ability to store charge per unit area and is typically expressed in microfarads per square centimeter (μF/cm² ). This value is relatively consistent across different types of neurons due to the uniform nature of the lipid bilayer that makes up the cell membrane.

Typical (Most Neurons): 0.5 to 1.0 uF/cm² - This range is fairly narrow because the capacitance is primarily determined by the physical properties of the lipid bilayer, which is similar in most biological membranes

Common The most commonly cited value for the specific membrane capacitance of neurons is around 1.0 μF/cm² , which is a widely used approximation in both experimental and computational neuroscience.

Factors Influencing CM

Membrane Composition: Minor variations in CM can occur due to differences in membrane thickness, composition of lipids, or the presence of embedded proteins, but these effects are usually minimal.
Experimental Conditions: Measurements can slightly vary based on the specific techniques used, such as patch-clamp or other electrophysiological methods.

Importance of Specific Membrane Capacitance:

Electrical Signaling: CM plays a crucial role in determining the time constant (τ) of a neuron, which affects how quickly the membrane potential can change in response to synaptic inputs.
Modeling Neuronal Behavior: In computational models, CM is a key parameter that, together with membrane resistance (RM), defines the passive electrical properties of neurons.

Actual Units

The quantities Rm, Ra, Cm, Vm, in the diagram and equation are given in Kilohm, Microfarad, or millivolts, and will depend on the size of the compartment. Note the use of lower case. This designates them as actual units.

Compartments are connected to each other through their axial resistances Ra. The axial resistance of a cylindrical compartment is proportional to its length and inversely proportional to its cross-sectional area.

For a piece of dendrite or a compartment of length l and diameter d we then have:

$R_{_{m}} = \frac{R_{M}}{π l d}$

$R_{a} = \frac{4 l R_{A}}{π d^{2}}$

$C_{m} = π l d C_{M}$

Sections of dendrite that have a continuous variation of voltage along the length are replaced by a "lumped parameter model" with discrete jumps in membrane potential. By using very many short compartments, the compartmental model can approach the result of the continuous cable equation. This is done by assuming that the values are the same in all compartments, as they are intrinsic properties of the neural membrane and cytoplasm. CM depends on the intrinsic properties of the thickness and dielectric constant of the membrane, and is usually close to 1uF/cm²

Time Constant (TM)

The time constant is a value in milliseconds that allows you to predict the percentage of the peak membrane voltage (Vm) at any point in time. The membrane time constant for a short uniform section is given by:

$T_{m} = R_{m} C_{m} = R_{M} C_{M}$

This Dendrite simulator calculates value of the membrane voltage at every millisecond point by applying the following formula $V_{m} = V_{s} + (V_{o} - V_{s}) e^{- t / R C}$

The time constant is modeled by a passive membrane resistance, Rm, a membrane capacitance, Cm, and a current source.

Where:

V_m is the compartment membrane voltage at time t
V_s is the height of the voltage step
V_o is the voltage on the capacitor at the last millisecond step
RC is the calculated time constant of the compartment

Note that the Time Constant (RC) is independent of the dimensions, because Rm is inversely proportional to the surface area, and Cm is proportional to the surface area.

Creating linked Synapse and Dendrites (8 minute YouTube video).

Video: Synapse and Dendrites

The exponential rise and decay of the membrane potential as the current traverses a section of leaky cable is shown in the next figure.

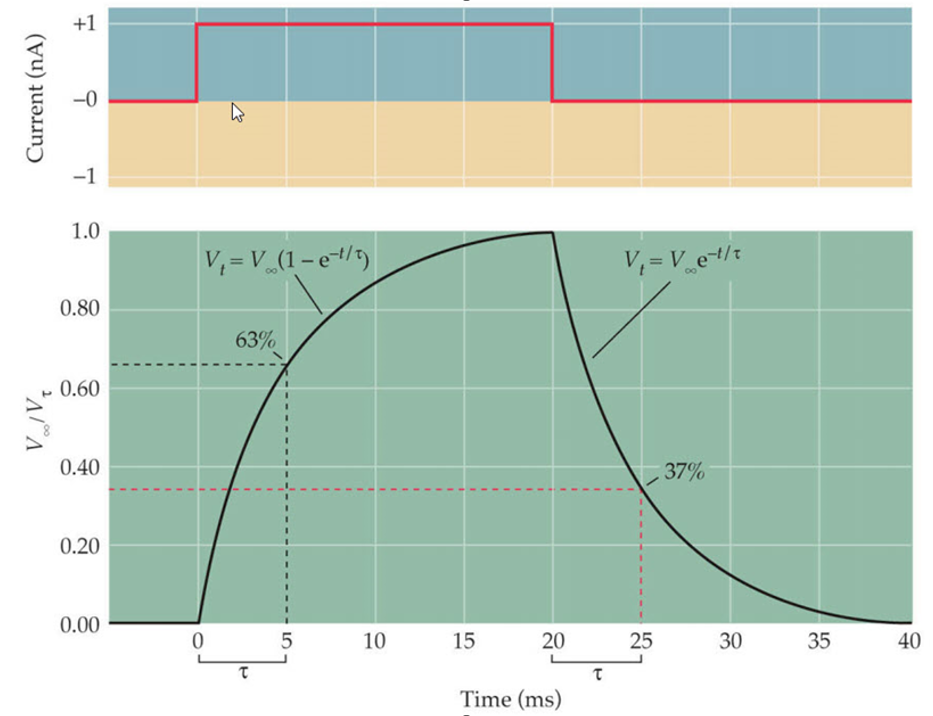
If you were to increase the leakage resistance R_m the slope would become more shallow. Conversely if the axial resistance R_axia_l were to increase you would get a sharper, faster drop in potential.

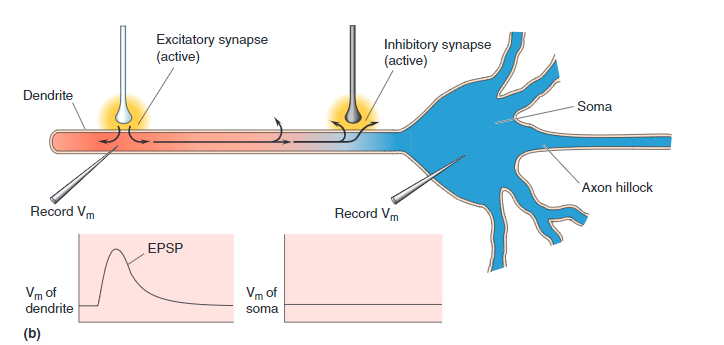
Excited and Depressed Dendrites

Connections from other neurons Axons may be attached to any one of thousands of places along the dendritic tree. The drawing of a compartment of dendrite (above) shows two types of ion channel connections:

EPSP, Green - If the connected ion channel stimulates the soma, it is called Excitatory Post-Synaptic Potential
IPSP, Red - If the connection channel depresses the downstream soma from firing it is called an Inhibitory Post-Synaptic Potential .

Each of these are connected through synapse. Leak channels shown in Orange are never connected.

EPSP Activated

IPSP Activated

This shows Step1 connected to an Inhibitory (IPSP) channel on Dendrite compartment 1. Step 4 is connected to an EPSP channel.

You can designate a Synapse as either EPSP or IPSP by right clicking the Synapse to view its parameters. There a radio button can be selected.

Minimum Firing Potential

Synaptic potentials produced by a single presynaptic neuron typically are not large enough to depolarize a postsynaptic cell to the threshold for an action potential to be generated in the Soma. The EPSPs produced in a motor neuron by most stretch-sensitive afferent neurons are only 0.2 to 0.4 mV in amplitude. If the EPSPs generated in a single motor neuron were to sum linearly, at least 25 afferent neurons would have to fire together and release transmitter to depolarize the trigger zone by the 10 mV required to reach threshold of firing by the Soma. [Kandel page 291 *]

Simulator

The best way to get a feel for the interaction of the various parameters of the dendrite is to run a simulation. Download and install the NeuronLab Simulator if you have not already (as described in section 3. NeuronLab Simulator).